Example Results
Results below might be reproduced from the following notebook. If you like you can try it yourself via the interactive version.
General Moran Model
We have designed four distinct systems based on well-known interaction examples which have been well-described in the literature [Tadelis-2012]:
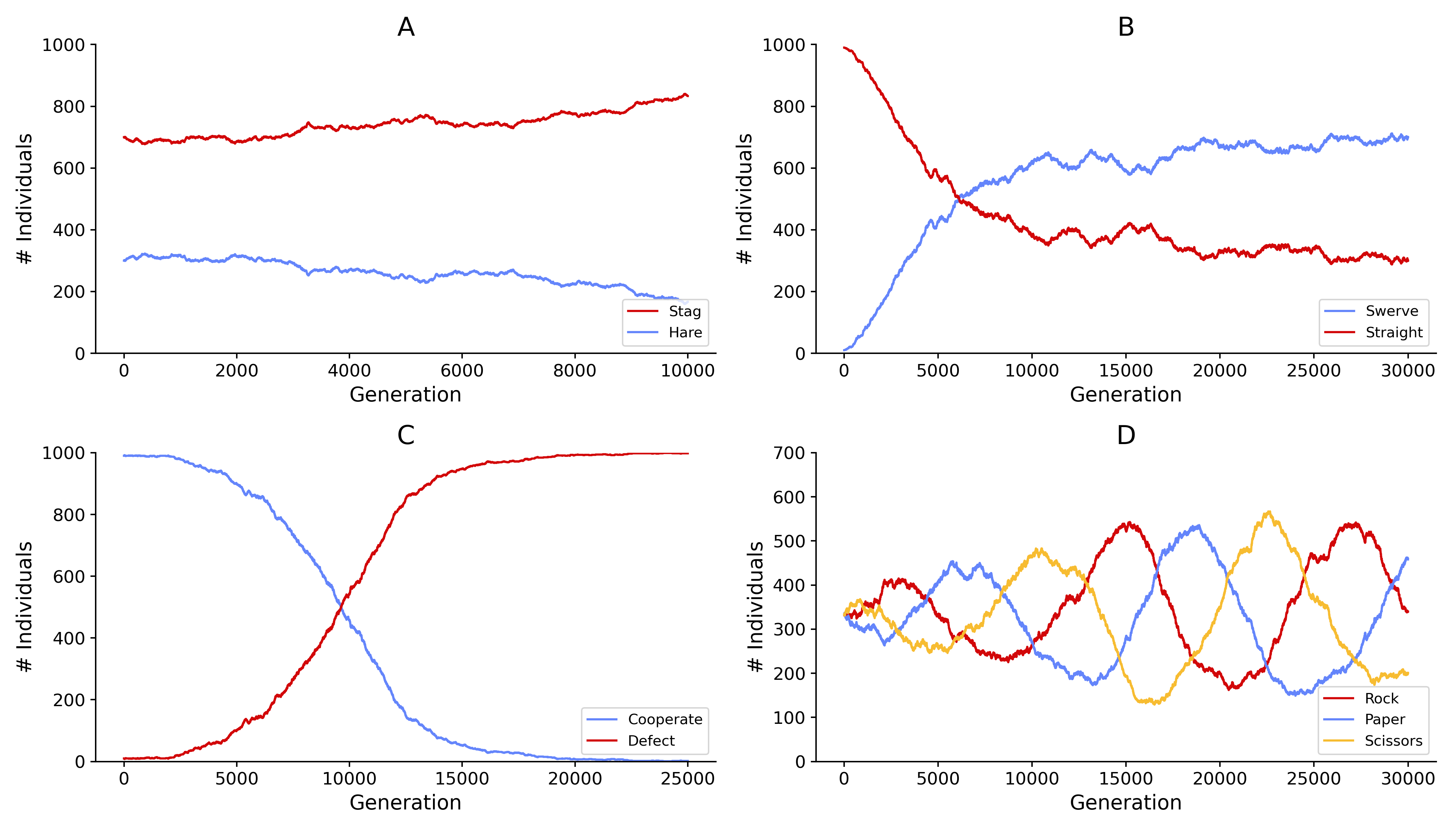
Simulations of population evolution based on: (A) Stag Hunt (B) Chicken game, (C) Prisoners’ Dilemma, (D) Rock Paper Scissors.
(A) The Stag Hunt game model describes a conflict between safety and social cooperation: the hare hunt represents small but certain profit, the stag hunt, great benefit but at great risk. Failure in cooperation leads to a player’s loss. There is no dominant strategy in this game as it is most beneficial for individuals to agree on the same strategy. Both stag hunt and hare hunt are evolutionarily stable strategies. A perfect example of this type of interaction is the “carousel feeding” behavior, a cooperative hunting method used by Norwegian orcas which forces a school of fish to form a tight ball; the orcas then stun fish with their tails [Fort-2007].
(B) In the game of Chicken a confrontational strategy brings a greater profit. However, if chosen by both individuals it yields the worst outcome. A peaceful strategy, while protecting against the greatest possible loss brings no reward when challenged by an aggressor. No player has a dominant strategy and there are no ESS in pure strategies in this game. Consider an example of two strains of the yeasts S. cerevisiae: wildtype and a mutant lacking the invertase gene. In a monosaccharide-poor environment yeasts may utilise invertase to produce an energy source from more complex molecules. Most monosaccharides are excreted to the extracellular environment from where they can also be taken up by other cells. Mutant strains (“cheaters”) follow a confrontational strategy: they consume glucose created by wildtype cells without bearing the metabolic cost of invertase production and secretion. Therefore, in a population, a confrontational strategy has a good advantage over the peaceful one, given the number of wildtype yeasts exceeds the number of mutants vastly. In case this condition is not met cheaters would fail to live off the others, leading to starvation - the worst possible scenario for them. Moreover, the analogy holds while inspecting the behaviour of wildtype yeasts. Trying to avoid that worst scenario, in the presence of mutants, wildtype cells cooperate in invertase expression over a wide range of conditions. However, when competing against other wildtype strains, invertase expression is repressed, causing them to exhibit the confrontational strategy - cheat [Gore-Youk-Oudenaarden-2009].
(C) Prisoners’ dilemma, often analyzed in game theory due to its multiple applications, presents a case where two completely rational individuals within incomplete knowledge might not cooperate, even if it appears that it is in their best interests to do so. The most rational strategy yields the worst collective outcome. Every participant has a dominant strategy. The only ESS is to always cooperate. In biological context the prisoner’s dilemma successfully captures the essential features of cancer growth and provides a framework for testing hypotheses and formulating claims in a quantitative manner [West-Hasnain-Macklin-Newton-2016]. In the case of malignant tumors, we observe the possibility of infiltration of adjacent tissues by cancer cells. Their characteristic uncontrolled proliferation leads to the growth of another tumor in this place and the destruction of healthy tissue.
(D) Rock-Paper-Scissors is a game with cyclic dominance resulting in oscillating populations of individuals among types. There is no ESS in this game. As an example, consider male side-blotched lizards, which come in three color morphs: orange, yellow, and blue. The orange males defend large territories. The yellow males can invade orange males’ territories. The blue male, in turn, effectively expels yellow males from their territory but are outcompeted by aggressive orange males [Sinervo-Lively-1996]. As a result: yellow beats orange, which bests blue which beats yellow.
References:
Moran Model based on 2D neighbourhood
Average payoff for an individual is calcualted based on interactions with 8 direct neighbours of a given individual (2D grid). Periodic boundary conditions are applied.
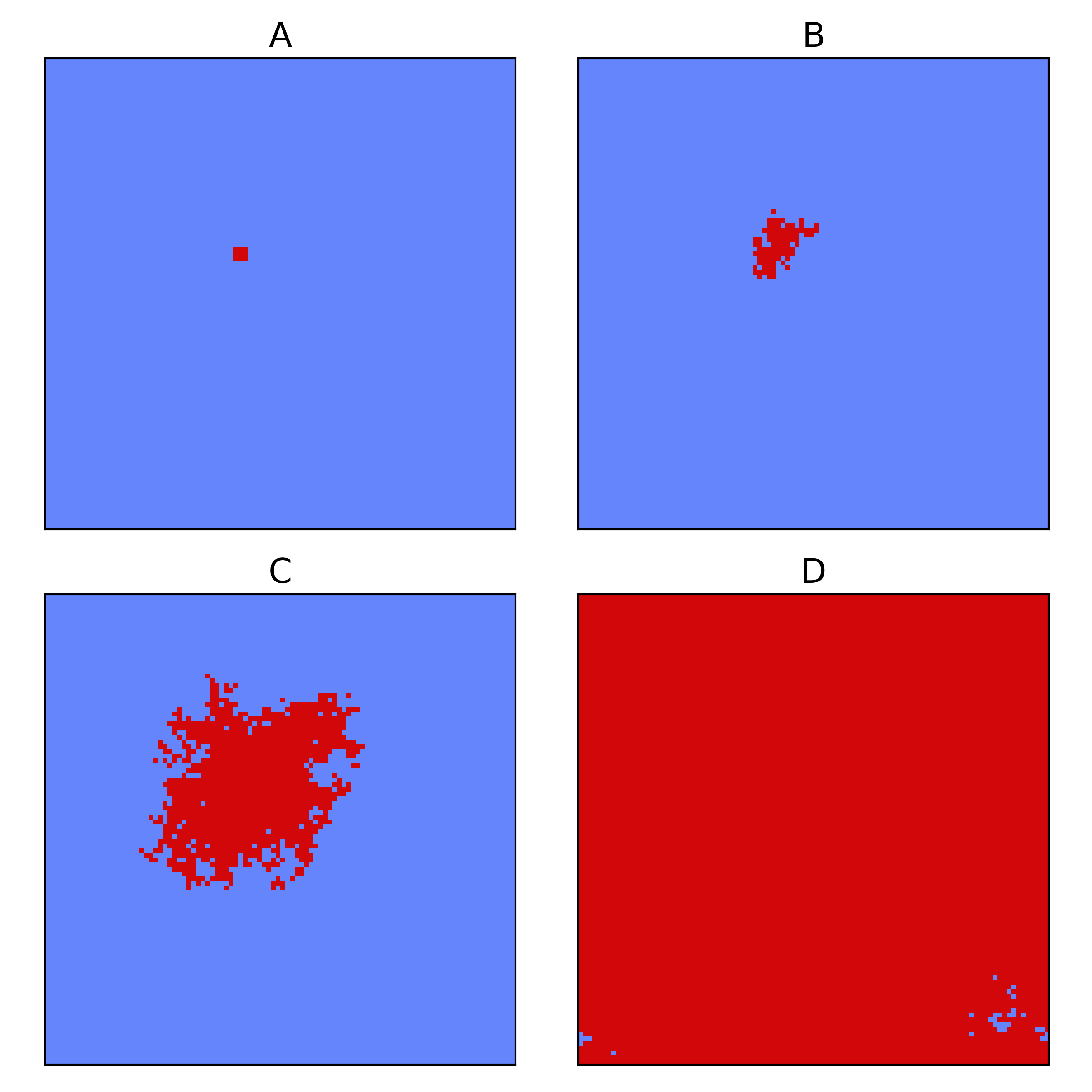
Population snapshots during an evolution according to a Prisoners Dilemma model. Starting from a small subpopulation of Defectors (A, t=0) we observe gradual growth (B, t=50000), (C, t=200000) until the whole population is almost completely overtaken (D, t=500000).
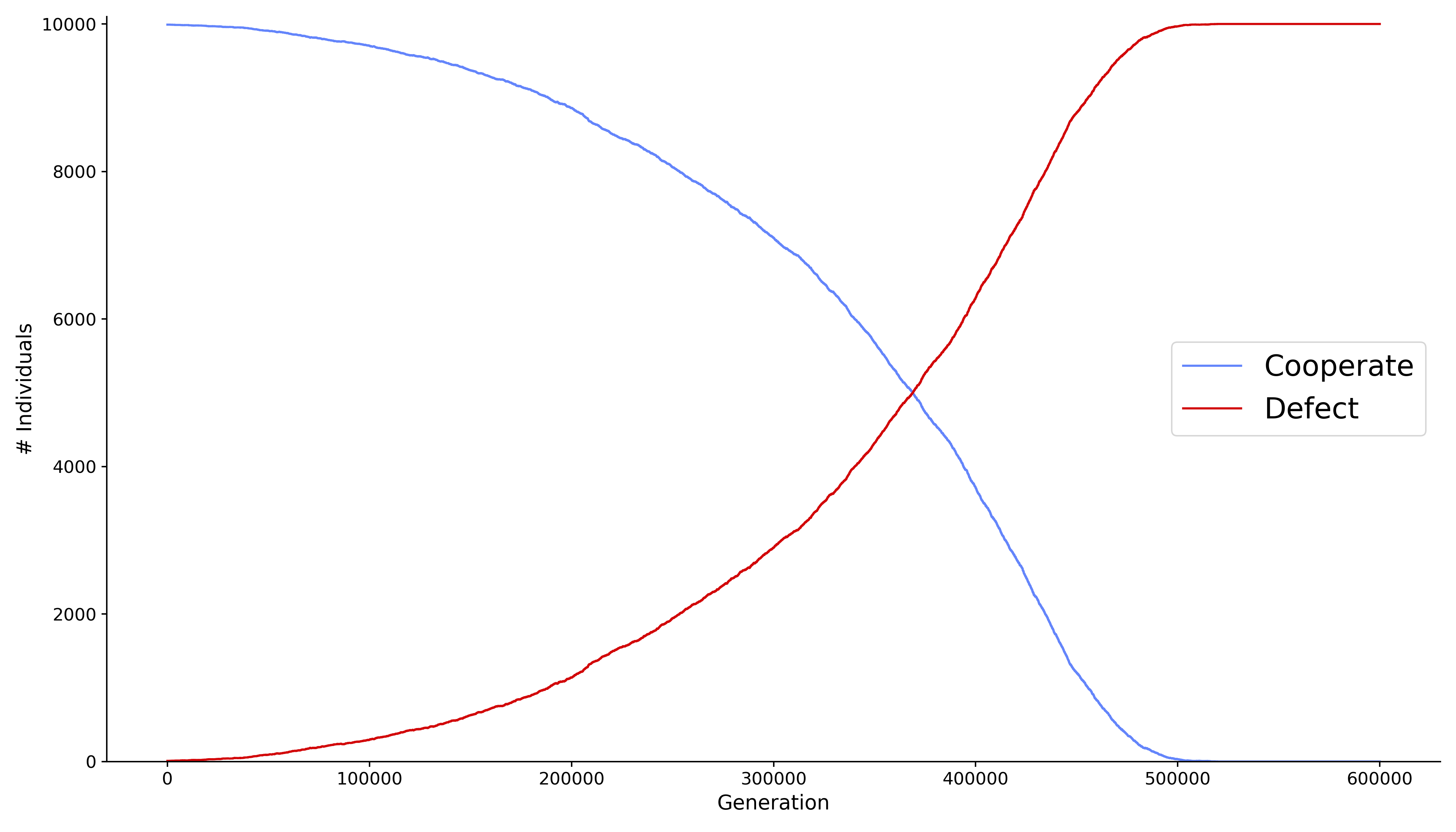
Growth curve for population evolution according to a Prisoners Dilemma model.
Moran Model based on 3D neighbourhood
Average payoff for an individual is calcualted based on interactions with 26 direct neighbours of a given individual (3D grid). Periodic boundary conditions are applied.
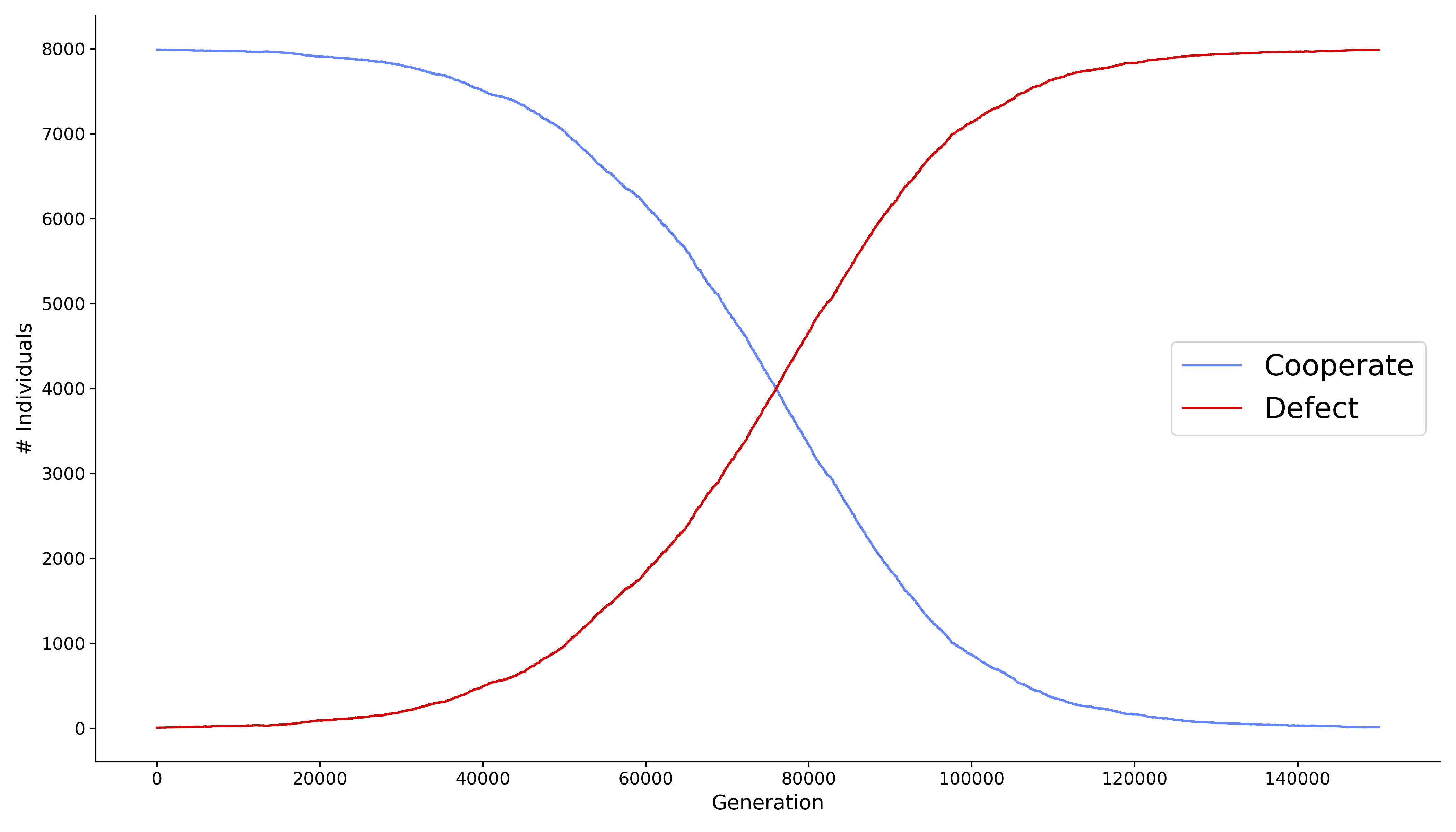
Growth curve for population evolution according to a Prisoners Dilemma model.